Buchak on risk and rationality

I'm very honoured to be part of the Author Meets Critics session on Lara Buchak's new book Risk and Rationality at the Pacific APA in San Diego this April (Buchak 2014).  It is a brilliantly insightful and closely argued book that I feel sure will be at the centre of a number of debates in decision theory over the next few years.  At the heart of the book is an alternative to expected utility theory that is intended to incorporate an agent's attitude to risk as a component of rational practical decision making along with the utilities and credences on which orthodox expected utility theory is based.  I'd like to write a series of posts about this alternative to orthodox expected utility theory that Buchak proposes.  So I'll start in this post with an overview of that alternative.  Needless to say, this is no substitute for reading the book, which is absolutely full of rich explanation and philosophical insights that demand a lot of reflection.

Expected utility

Let us begin with the framework in which Buchak formulates both expected utility theory and her own alternative to it.  There are three main ingredients to the background framework:

• $\mathcal{S}$ is the set of states (or possible worlds). Degrees of belief or credences will be assigned to a $\sigma$-algebra $\mathcal{F}$ of subsets of $\mathcal{S}$:  these are propositions represented as sets of states or possible worlds.
• $\mathcal{X}$ is the set of outcomes.  Utilities will be assigned to the elements of $\mathcal{X}$.
• $\mathcal{A}$ is the set of acts.  These are finite-valued functions from $\mathcal{S}$ to $\mathcal{X}$.  Thus, we can represent an act $f \in \mathcal{A}$ as $f = \{x_1, E_1; \ldots; x_n, E_n\}$, where $x_1, \ldots, x_n$ are the values of $f$ and $E_i$ is the proposition that $f$ will have outcome $x_i$ (we assume that this proposition is in $\mathcal{F}$)---that is, $E_i = f^{-1}(x_i) = \{s \in \mathcal{S} : f(s) = x_i\}$.  For each outcome $x \in \mathcal{X}$, there is an act $[x] \in \mathcal{A}$ such that $[x](s) = x$ for all states $s \in \mathcal{S}$.  We call this the constant act on $x$.  Let $[\mathcal{X}] = \{[x] : x \in \mathcal{X}\} \subseteq \mathcal{A}$ be the set of constant acts.

For instance, suppose our agent is choosing between two options:  on the first, which we will call Safe, she is guaranteed to receive £50; on the second, which we will call Risky, a fair coin will be flipped and she will receive £100 if the coin lands heads and £0 if the coin lands tails.  Then:

• The set of states may be taken to be $\mathcal{S}$ = {Heads, Tails};
• The set of outcomes may be taken to be $\mathcal{X} = \{£0, £50, £100\}$;
• The two options between which our agent is choosing belong to the set $\mathcal{A}$ of acts.  They are Safe = {Heads $\vee$ Tails}, £50} and Risky = {Heads, £100; Tails, £0}.  Note that Safe = [£50]; that is, Safe is the constant act on £50.

With this framework in place, we can state the business of decision theory.  It is concerned with the relationship between two sorts of attitudes:  external attitudes and internal attitudes.  The external attitudes are typically taken to be given by the agent's pairwise preferences over the set $\mathcal{A}$ of acts.  The internal attitudes are typically taken to be given by the agent's credences in propositions in a $\sigma$-algebra $\mathcal{F}$ on $\mathcal{S}$ and her utilities for outcomes in $\mathcal{X}$:  however, one of Buchak's central contentions is that there is a third type of internal attitude with which decision theory deals, namely, attitudes to risk.  If one is a constructivist about the internal attitudes, then one will take only the external attitudes to be real:  one will then take the business of decision theory to be the representation of the external attitudes by treating the agent as if she has internal attitudes and as if she combines those attitudes in a particular way to give her external attitudes.  If one is a realist about the internal attitudes, then one will take both sorts of attitudes to be real:  one will then say that a rational agent's internal and external attitudes ought to relate in a particular way; indeed, they ought to relate as if she obtains her external attitudes by combining her internal attitudes in a particular way.

Expected utility theory posits only two types of internal attitudes: these are given by the agent's credences and utilities.  Her credences measure how strongly she believes the propositions in $\mathcal{F}$:  they are given by a probability function $p : \mathcal{F} \rightarrow [0, 1]$.  Her utilities measure how strongly she desires or values the outcomes in the set $\mathcal{X}$:  they are given by a utility function $u : \mathcal{X} \rightarrow \mathbb{R}$.  As with most decision theories, expected utility theory posits one type of external attitude: this is given by the agent's preference ordering, which is a binary relation $\succeq$ on the set of acts $\mathcal{A}$;  $f \succeq g$ says that the agent weakly prefers $f$ to $g$.  Expected utility theory then employs the following rule of combination, which states how her internal and external attitudes ought to relate:

The EU rule of combination Suppose $f = \{E_1, x_1; \ldots; E_n, x_n\}$.  Then let
$$EU_{p, u}(f) = \sum^n_{i=1} p(E_i)u(x_i)$$
Then it ought to be that
$$f \succeq g \Longleftrightarrow EU_{p, u}(f) \geq EU_{p, u}(g)$$

That is, an agent's preferences ought to order acts by their subjective expected utility.

Thus, for instance, consider the act $h = \{E_1, x_1; \ldots; E_4, x_4\}$, where
$$u(x_1) = 3, u(x_2) = 5, u(x_3) = 5, u(x_4) = 6$$
and
$$p(E_1) = 0.3, p(E_2) = 0.2, p(E_3) = 0.1, p(E_4) = 0.4$$
Then the following figure illustrates the expected utility of $h$.

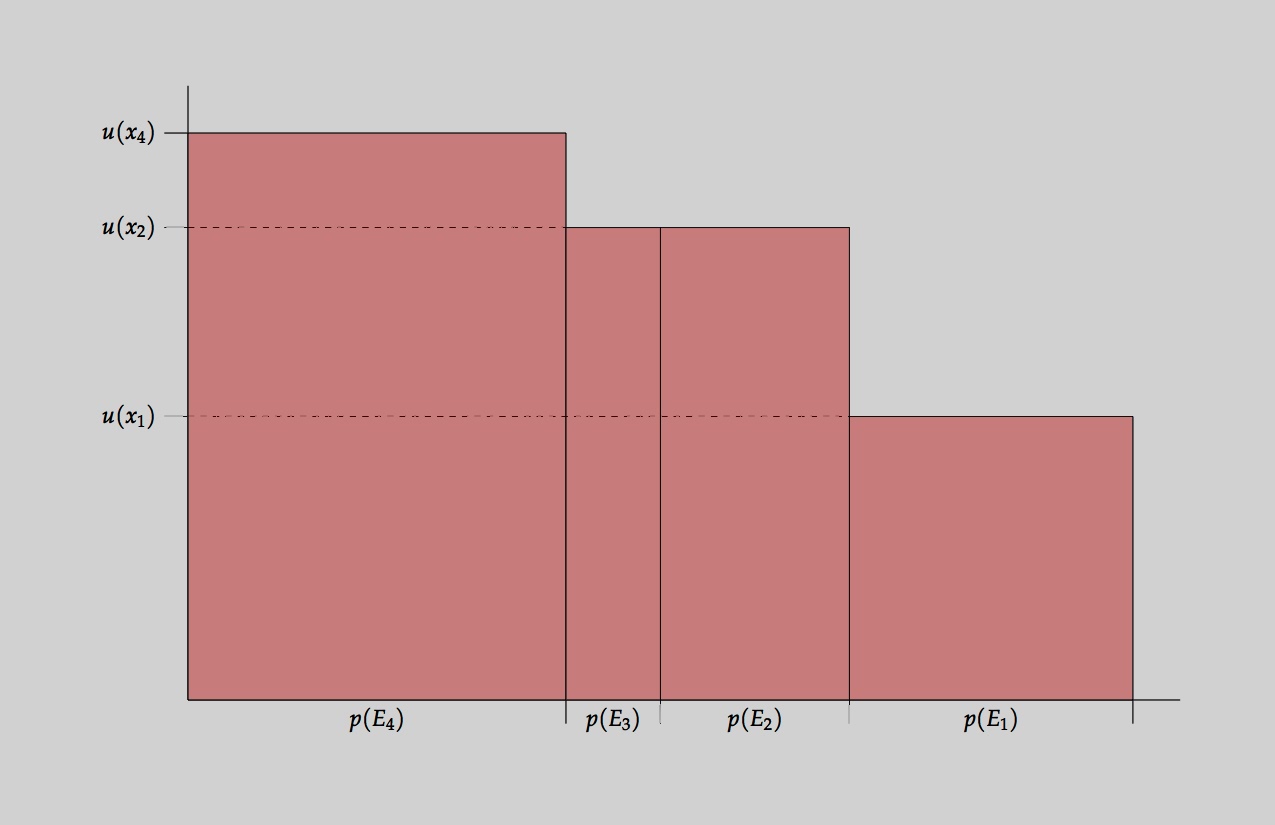Fig. 1:  $EU_{p, u}(h)$ is obtained by summing the areas of the four vertical rectangles:  each area is $p(E_i)u(x_i)$.

It is obtained by taking a weighted sum of the utilities of the possible outcomes, where the weight given to a particular outcome is given by the probability that the outcome will result from $h$.

Fig. 1 suggests two ways in which we might reformulate $EU_{p, u}(f)$.  These will be very useful in understanding how expected utility theory relates to Buchak's proposal.

First reformulation First, it is clear that $EU_{p, u}(f)$ depends only on the utilities of the outcomes to which the act $f$ may give rise and the probabilities that $f$ will produce outcomes with those utilities.  Thus, given an act $f = \{E_1, x_1; \ldots; E_n, x_n\}$ and a utility function $u$, we might redescribe $f$ as $\{F_1, u_1; \ldots; F_k, u_k\}$ where

• $u_1, \ldots, u_k$ are the utilities to which $f$ might give rise ordered from least to greatest---that is, $u_1 < \ldots < u_k$.  For instance, in our example act $h$: $u_1 = 3$, $u_2 = 5$, $u_3 = 6$.
• $F_j$ is the proposition that $f$ will give rise to $u_j$.  For instance, in our example act $h$: $F_1 \equiv E_1$, $F_2 \equiv E_2 \vee E_3$, $F_3 \equiv E_4$.

We call this the ordered utility-based description of $f$ relative to $u$.

Then
$$EU_{p, u}(f) = \mathcal{S}um^k_{j=1} p(F_j)u_j$$
Then Fig. 2 illustrates this reformulation of expected utility for our example act $h$.

Fig. 2: $EU_{p, u}(h)$ of $h$ is obtained by summing the areas of the three vertical rectangles (the middle two vertical rectangles from Fig. 1 have been merged): each area is $P(F_j)u_j$.

Second reformulation The second reformulation of $EU_{p, u}(f)$ builds on this first and is illustrated in Fig. 3.  Suppose $f = \{F_1, u_1; \ldots; F_k, u_k\}$ is the ordered utility-based description of $f$ relative to $u$.  Then
$$EU_{p, u}(f) = u_1 + \sum^k_{j=2} p(F_j \vee \ldots \vee F_k)(u_j - u_{j-1})$$
Again, the expected utility of an act is given by a weighted sum:  but this time the quantities to be weighted are the differences between one possible utility and the possible utility immediately below it; and the weight assigned to that difference is the probability that the act will give rise to at least that much utility.

$EU_{p, u}(h)$ is obtained by summing the areas of the three horizontal rectangles.  Their areas are $p(F_1 \vee F_2 \vee F_3)u_1 = u_1$, $p(F_2 \vee F_3)(u_2 - u_1)$, and $p(F_3)(u_3 - u_2)$.

 

Risk-weighted expected utility

With this in hand, we're ready to formulate Buchak's alternative to expected utility theory.  Buchak is motivated by the apparent rationality of risk-sensitive behaviour.  Notoriously, some seemingly rational risk-sensitive behaviour cannot be captured by expected utility theory at all:  for instance,  Allais described seemingly rational preferences that cannot be generated by any rational credence function and utility function in the way prescribed by expected utility theory (Allais 1953).  Moreover, there are other seemingly rationally preferences that can be generated by a credence function and utility function in line with expected utility theory, but which seem to be rational even for agents who do not have credences and utilities that would generate them in this way.  Thus, for instance, consider the two acts described at the beginning of this section:  Safe = {Heads $\vee$ Tails}, £50} and Risky = {Heads, £100; Tails, £0}.  Suppose that our agent strictly prefers Safe to Risky:  that is, Safe $succ$ Risky.  Can expected utility theory capture the rationality of this preference?  Suppose that, since the coin is known to be fair, rationality requires that the agent assign $p$(Heads) = 0.5 = $p$(Tails).  Then it is still possible to describe a utility function on the outcomes £0, £50, £100 that generates these preferences in the way expected utility theory requires.  Let $u(£0) = 0$ and $u(£100 = £50 + £50) < u(£50) + u(£50)$.  That is, suppose the agent treats money as a dependent good:  how much utility it gives depends on how much of it she has already; so, money has diminishing marginal utility for this agent.  Then, for an agent with this credence function and utility function, $EU_{p, u}$(Safe) > $EU_{p, u}$(Risky), as required.  So expected utility theory can capture the rationality of these preferences.  However, as Buchak rightly observes, those preferences seem rational not only for an agent for whom money has diminishing marginal utility; they seem rational even for an agent whose utility is linear in money.  And this is something that expected utility cannot capture.  Thus, Buchak is interested not only in saving the Allais preferences, but also in saving other risk-sensitive behaviour without attributing the risk-sensitive behaviour to the shape of the utility function.

How does Buchak hope to capture these risk-sensitive preferences?  Where expected utility theory countenances only two types of internal attitude as relevant to preferences, Buchak countenances a third as well:  this third component is supposed to capture the agent's attitude to risk, and it is given by a function $r : [0, 1] \rightarrow [0, 1]$, which Buchak assumes to be strictly increasing, continuous, and taking the following values, $r(0) = 0$ and $r(1) = 1$.  (As Buchak explains, her proposal is closely related to proposals by (Quiggin 1982), (Machina & Schmeidler, 1992), and (Köbberling & Wakker, 2003)).

Buchak's risk-weighted expected utility theory then employs the following rule of combination, which states how an agent's internal and external attitudes ought to relate, where the agent has credence function $p$, utility function $u$, and risk function $r$:

The REU rule of combination  Suppose $f = \{F_1, u_1; \ldots; F_k, u_k\}$ is the ordered utility-based description of $f$ relative to $u$.  Then let
$$REU_{r, p, u}(f) = u_1 + \sum^k_{j=2} r(p(F_j \vee \ldots \vee F_k))(u_j - u_{j-1})$$
Then it ought to be that
$$f \succeq g \Longleftrightarrow REU_{r, p, u}(f) \geq REU_{r, p, u}(g)$$

In Fig. 4, we illustrate the risk-weighted expected utility of our example act $h$ when the agent has the risk function $r_2(x) := x^2$.

Fig. 4: $REU_{r_2, p, u}(h)$ is given by the grey area, where $r_2(x) := x^2$

Notice that the formulation of $REU_{r, p, u}(f)$ is exactly like the formulation of $EU_{p, u}(f)$ that we gave above except that each probability weight is transformed by the agent's risk function.  Thus, if $r(x) < x$ (for all $0 < x < 1$), then, as Fig. 4 illustrates, the lowest utility to which the act can give rise--namely, $u_1$--contributes just as much to $REU_{r, p, u}(f)$ as it does to $EU_{p, u}(f)$--it contributes $u_1$ to both. But further increases in utility--such as the increase from minimum utility of $u_1$ to minimum utility of $u_2$--make less of a contribution since their probability--$p(F_2 \vee F_3)$--is acted on by the risk function, and it is this reduced value--$r(p(F_2 \vee F_3))$--that weights the possible increases in utility.  Thus, such an agent displays risk-averse behaviour. $r_2$ is such a risk function.

Similarly, if $r(x) > x$ (for all $0 < x < 1$), then the lowest utility to which the act can give rise contributes just as much to $REU_{r, p, u}(f)$ as it does to $EU_{p, u}(f)$, but further increases in utility make more of a contribution since their probability is acted on by the risk function and it is this increased value that weights the possible increases in utility.  This is illustrated in Fig. 5.  Such an agent displays risk-seeking behaviour.  $r_{0.5}(x) := \sqrt{x}$ is such a risk function.

$REU_{r_{0.5}, p, u}(h)$ is given by the grey area, where $r_{0.5}(x) := \sqrt{x}$

It's also easy to see that, if $r_1(x) := x$ (for $0 \leq x \leq 1$), then $REU_{r_1, p, u}(f) = EU_{p, u}(f)$.  Thus, expected utility theory is the special case of risk-weighted expected utility theory given by a linear risk function.  In such a situation, we say that the agent is risk-neutral.  This means that Buchak's theory permits any preferences that expected utility theory permits.  But it also permits a whole lot more.  For instance, one can easily recover the Allais preferences or the preference Safe $\succ$ Risky described above by attributing to an agent a certain sort of risk function--in both cases, a risk-averse risk function.

This, then, is Buchak's proposal.  In the book, she presents a representation theorem for the REU rule of combination.  That is, she presents axioms for a preference ordering such that $\succeq$ satisfies those axioms iff there is a unique probability function $p$, a unique risk function $r$, and a unique-up-to-affine-transformation utility function $u$ such that
$$f \succeq g \Longleftrightarrow REU_{r, p, u}(f) \geq REU_{r, p, u}(g)$$
She also defends her proposal as the only way to understand risk-sensitive agents that still interprets them as engaged in means-end or instrumental reasoning.  I hope to write more about the latter topic in the next post.

References

• Allais, M. (1953). Le comportement de l’homme rationnel devant le risque: critique des postulats et axiomes de l’école Américaine. Econometrica, 21(4):503-546.
• Buchak, L. (2014). Risk and Rationality. Oxford University Press.
• Köbberling, V. & P. Wakker (2003). Preference Foundations for Nonexpected Utility Theory: A Generalized and Simplified Technique. Mathematics of Operations Research, 28(3):39-423
• Machina, M. J. & D. Schmeidler (1992) A More Robust Definition of Subjective Probability. Econometrica, 60(4):745-80.
• Quiggin, J. (1982) A Theory of Anticipated Utility. Journal of Economic Behavior and Organization, 3:323-43.