Posts

Showing posts from February, 2014
Show All
Posted by

Job opportunities at the MCMP

1 comment
Posted by

The deductive use of logic in mathematics (Part III of 'Axiomatizations of arithmetic...')

2 comments
Posted by

The descriptive use of logic in mathematics (Part II of 'Axiomatizations of arithmetic...')

7 comments
Posted by

Axiomatizations of arithmetic and the first-order/second-order divide

3 comments
Posted by

CFP: Symposium on the Foundations of Mathematics, 7-8 July, Kurt Gödel Research Center, Vienna.

Post a Comment
Posted by

Summer School on PROBABILITIES IN PHYSICS (July 21-26, 2014)

Post a Comment
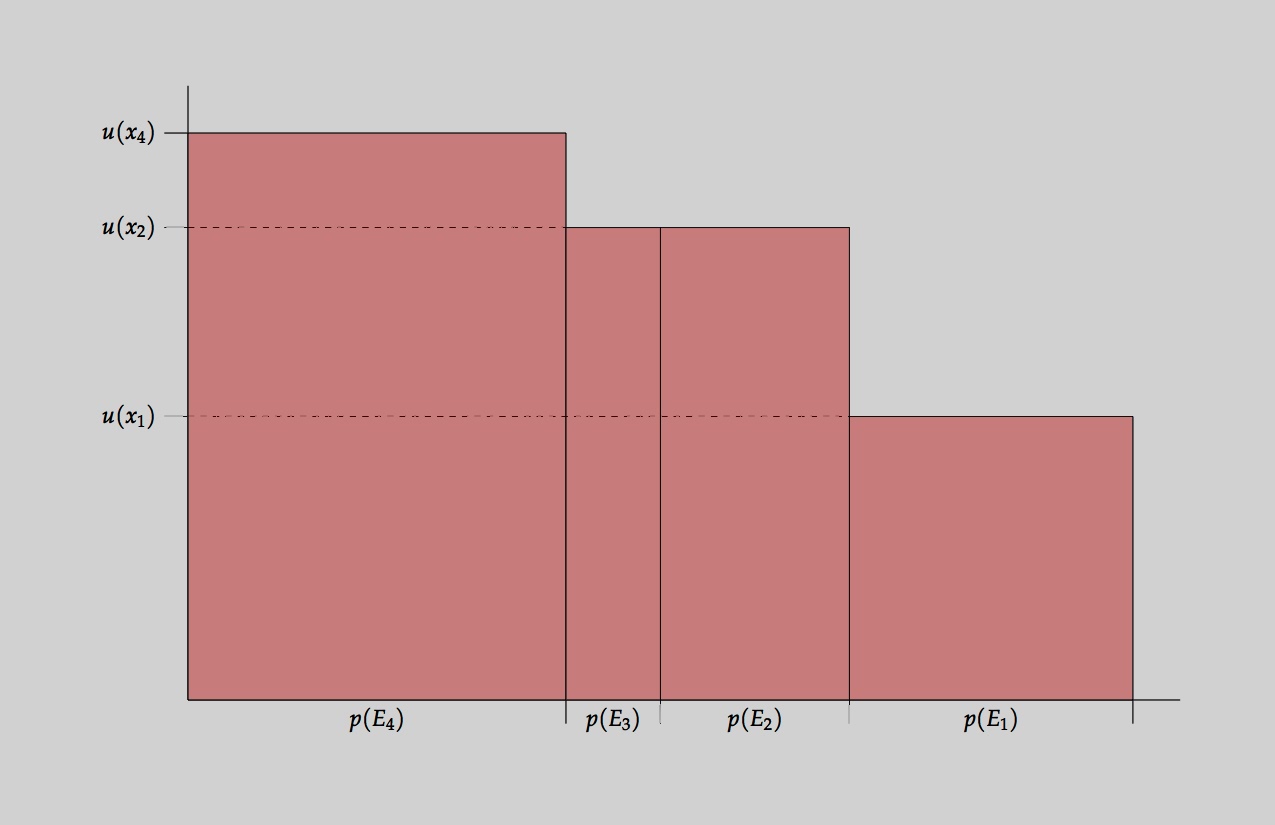
Image
Posted by

Buchak on risk and rationality

1 comment