Dutch Books and Conditionalization
I've just signed a contract with Cambridge University Press to write a book on the Dutch Book Argument
for their Elements in Decision Theory and Philosophy series. So over
the next few months, I'm going to be posting some bits and pieces as I
get properly immersed in the literature.
-------
In this post, I'm interested in Dutch Book or sure loss arguments for updating norms, which say how you should change your credences in response to new evidence.
Roughly speaking, there are two sorts of updating norm: the first governs actual features of your updating behaviour, such as the credence function you actually adopt after receiving new evidence; the second governs both actual and counterfactual features of your updating behaviour, such as the credence function you would adopt or the credence functions you might adopt were you to learn one thing, the credence function you would adopt or the credence functions you might adopt were you to learn some other thing. As we will see, there are no good sure loss arguments for the first sort of norm. We'll see this in two ways. First, we'll see that, while there's one sort of sure loss that you are vulnerable to if you actually don't update in the prescribed way, you are also vulnerable to this if you actually do update in the prescribed way. Second, we'll see that, while there's a second sort of sure loss that doesn't have the problems of the first, it is possible actually to update in the prescribed way and yet still be vulnerable to this sort of sure loss (if you wouldn't have updated in the prescribed way had you learned something other than what you actually learned), and it is possible to not actually update in the prescribed way and yet nonetheless not be vulnerable to this sort of sure loss (if you might have updated differently in the light of the evidence you actually received, and if those other possible updates differ from your actual update in a certain way).
To illustrate these points, let's pursue an example throughout the chapter. Consider Sandy. On Monday, Sandy is 40% confident that the global mean surface temperature will rise by between 0 and 1 degrees Celsius in the next 100 years. That is his unconditional credence in the proposition Medium on Monday. As well as that unconditional credence, he also has various conditional credences on Monday. For instance, let CO$_2$ High be the proposition that current CO$_2$ levels are greater than 420ppm, and let CO$_2$ Low be its negation. On Monday, Sandy has a conditional credence in Medium given CO$_2$ High---it is 60%. And he has a conditional credence in Medium given CO$_2$ Low---it is 20%. By definition, his conditional credence in one proposition $A$ given another $B$ is the proportion of his credence in $B$ he gives also to $A$. That is, it is the ratio of his credence in the conjunction $A\ \&\ B$ to his credence in $B$. Now, on Tuesday, Sandy learns CO$_2$ High. In the light of this, he updates his credences. His new unconditional credence in Medium is 70%. We naturally judge him irrational. If he were rational, his unconditional credences on Tuesday would be the same as his conditional credences on Monday given CO$_2$ High, the proposition he gained as evidence in between times. In the jargon, he would update by conditionalizing on his new evidence, CO$_2$ High. But he doesn't.
So Sandy violates a putative norm that governs his actual updating behaviour:
Roughly speaking, there are two sorts of updating norm: the first governs actual features of your updating behaviour, such as the credence function you actually adopt after receiving new evidence; the second governs both actual and counterfactual features of your updating behaviour, such as the credence function you would adopt or the credence functions you might adopt were you to learn one thing, the credence function you would adopt or the credence functions you might adopt were you to learn some other thing. As we will see, there are no good sure loss arguments for the first sort of norm. We'll see this in two ways. First, we'll see that, while there's one sort of sure loss that you are vulnerable to if you actually don't update in the prescribed way, you are also vulnerable to this if you actually do update in the prescribed way. Second, we'll see that, while there's a second sort of sure loss that doesn't have the problems of the first, it is possible actually to update in the prescribed way and yet still be vulnerable to this sort of sure loss (if you wouldn't have updated in the prescribed way had you learned something other than what you actually learned), and it is possible to not actually update in the prescribed way and yet nonetheless not be vulnerable to this sort of sure loss (if you might have updated differently in the light of the evidence you actually received, and if those other possible updates differ from your actual update in a certain way).
To illustrate these points, let's pursue an example throughout the chapter. Consider Sandy. On Monday, Sandy is 40% confident that the global mean surface temperature will rise by between 0 and 1 degrees Celsius in the next 100 years. That is his unconditional credence in the proposition Medium on Monday. As well as that unconditional credence, he also has various conditional credences on Monday. For instance, let CO$_2$ High be the proposition that current CO$_2$ levels are greater than 420ppm, and let CO$_2$ Low be its negation. On Monday, Sandy has a conditional credence in Medium given CO$_2$ High---it is 60%. And he has a conditional credence in Medium given CO$_2$ Low---it is 20%. By definition, his conditional credence in one proposition $A$ given another $B$ is the proportion of his credence in $B$ he gives also to $A$. That is, it is the ratio of his credence in the conjunction $A\ \&\ B$ to his credence in $B$. Now, on Tuesday, Sandy learns CO$_2$ High. In the light of this, he updates his credences. His new unconditional credence in Medium is 70%. We naturally judge him irrational. If he were rational, his unconditional credences on Tuesday would be the same as his conditional credences on Monday given CO$_2$ High, the proposition he gained as evidence in between times. In the jargon, he would update by conditionalizing on his new evidence, CO$_2$ High. But he doesn't.
So Sandy violates a putative norm that governs his actual updating behaviour:
Actual Conditionalization If
- $c$ is your credence function at $t$,
- $c'$ is your credence function at a later time $t'$,
- $E$ is the strongest evidence you obtained between $t$ and $t'$, and
- $c(E) > 0$,
then it ought to be that $c'(X) = c(X | E)$, for all $X$.
Is there a sure loss argument against Sandy? As we said at the beginning, there is one sort of sure loss argument against him, but this proves too much; there is also another sort of sure loss argument, but it does not apply to Sandy only on the basis of his actual updating behaviour---if it applies to him at all, it is on the basis of other modal features of him.
Throughout, we'll assume that Sandy's credences are probabilistic on Monday and probabilistic on Tuesday. As a result, the Converse Dutch Book Theorem tells us that there is no Dutch Book that can be made against his credences on Monday and no Dutch Book that can be made against his credences on Tuesday. Perhaps, though, there is some sort of Dutch Book we can make against the combination of his credences at the two different times. That is, perhaps there is a diachronic Dutch Book against Sandy. This would consist of a set of bets offered on Monday and a set of bets offered on Tuesday; his Monday credences would have to require him to accept the Monday bets and his Tuesday credences would have to require him to accept the Tuesday bets; and, taken together, those bets would be guaranteed to lose him money. We might say that you are irrational if you are vulnerable to a diachronic Dutch Book.
In fact, it turns out that there is such a diachronic Dutch Book against Sandy. His credences require him to sell a £100 bet on Medium for £45 on Monday, since he's 40% confident in Medium on Monday. And they require him to buy a £100 bet on Medium for £55 on Tuesday, since he's 70% confident in Medium on Tuesday. Taken together, these two bets will lose Sandy £10 in all epistemically possible worlds. Thus, if vulnerability to a diachronic Dutch Book is sufficient for irrationality, then Sandy is irrational.
The problem with this argument is that Sandy is also required to accept that same pair of bets on Monday and Tuesday if he updates by conditionalizing on the evidence he learns, namely, $E$. In that case, his credences on Monday are the same as before and thus require him to sell a £100 bet on Medium for £45 on Monday. And his credence in Medium on Tuesday is 60%, rather than 70%, and that still requires him to pay £55 for a £100 bet on Medium. So he is sure to lose £10. And indeed, unless he retains exactly the same credences between Monday and Tuesday, there will always be a pair of bets, one offered on Monday that his Monday credences require him to accept, and one offered on Tuesday that his Tuesday credences require him to accept, that, taken together, will lose him money at all epistemically possible worlds. So, if vulnerability to a diachronic Dutch Book is sufficient for irrationality, then Sandy is irrational, but so is anyone who ever changes any of their credences. And that surely can't be right.
So the existence of a diachronic Dutch Book against your actual updating behaviour is not sufficient for irrationality. But why not? One natural answer is this. Come Tuesday, both we and Sandy know that he in fact learned CO$_2$ High (which we'll call $E$) and updated his credence in Medium (which we'll abbreviate $M$) on the basis of that. But, on Monday, it is still open at least from Sandy's own point of view which of $E$ or $\overline{E}$ he will learn. And, were he to learn $\overline{E}$ instead, he might well have updated his credences in a different way.
Throughout, we'll assume that Sandy's credences are probabilistic on Monday and probabilistic on Tuesday. As a result, the Converse Dutch Book Theorem tells us that there is no Dutch Book that can be made against his credences on Monday and no Dutch Book that can be made against his credences on Tuesday. Perhaps, though, there is some sort of Dutch Book we can make against the combination of his credences at the two different times. That is, perhaps there is a diachronic Dutch Book against Sandy. This would consist of a set of bets offered on Monday and a set of bets offered on Tuesday; his Monday credences would have to require him to accept the Monday bets and his Tuesday credences would have to require him to accept the Tuesday bets; and, taken together, those bets would be guaranteed to lose him money. We might say that you are irrational if you are vulnerable to a diachronic Dutch Book.
In fact, it turns out that there is such a diachronic Dutch Book against Sandy. His credences require him to sell a £100 bet on Medium for £45 on Monday, since he's 40% confident in Medium on Monday. And they require him to buy a £100 bet on Medium for £55 on Tuesday, since he's 70% confident in Medium on Tuesday. Taken together, these two bets will lose Sandy £10 in all epistemically possible worlds. Thus, if vulnerability to a diachronic Dutch Book is sufficient for irrationality, then Sandy is irrational.
The problem with this argument is that Sandy is also required to accept that same pair of bets on Monday and Tuesday if he updates by conditionalizing on the evidence he learns, namely, $E$. In that case, his credences on Monday are the same as before and thus require him to sell a £100 bet on Medium for £45 on Monday. And his credence in Medium on Tuesday is 60%, rather than 70%, and that still requires him to pay £55 for a £100 bet on Medium. So he is sure to lose £10. And indeed, unless he retains exactly the same credences between Monday and Tuesday, there will always be a pair of bets, one offered on Monday that his Monday credences require him to accept, and one offered on Tuesday that his Tuesday credences require him to accept, that, taken together, will lose him money at all epistemically possible worlds. So, if vulnerability to a diachronic Dutch Book is sufficient for irrationality, then Sandy is irrational, but so is anyone who ever changes any of their credences. And that surely can't be right.
So the existence of a diachronic Dutch Book against your actual updating behaviour is not sufficient for irrationality. But why not? One natural answer is this. Come Tuesday, both we and Sandy know that he in fact learned CO$_2$ High (which we'll call $E$) and updated his credence in Medium (which we'll abbreviate $M$) on the basis of that. But, on Monday, it is still open at least from Sandy's own point of view which of $E$ or $\overline{E}$ he will learn. And, were he to learn $\overline{E}$ instead, he might well have updated his credences in a different way.
Let's suppose he would. In fact, contrary to the description of the example so far, let's suppose that, whichever he learns, he'll update by conditionalizing. So, if he learns $E$, he'll become 60% confident in $M$, and if he learns $\overline{E}$, he'll become 20% confident in $M$. Then his Monday credences require him to sell a £100 bet on $M$ for £45, and his Tuesday credences should he learn $E$ require him to buy a £100 bet on $M$ for £55, thereby losing him money whether or not $M$ is true. But his Tuesday credences should he learn $\overline{E}$ do not require him to buy a £100 bet on $M$ for £55. Indeed, they require him to refuse to buy that bet.
This suggests the following sort of argument against someone who will update by something other than conditionalizing in the face of some evidence they might acquire. Suppose $c$ is your credence function at time $t$---it is defined on $\mathcal{F}$. There's some proposition $E$ in $\mathcal{F}$ that you might learn as evidence between an earlier time $t$ and a later time $t'$. And you'll learn $E$ just in case it's true. And suppose $c(E) > 0$. If you learn $E$---that is, if $E$ is true---you'll adopt credence function $c'$. If you don't learn $E$---that is, if $E$ is false---we don't know how you'll respond---perhaps it isn't determined. Then we'll say that you are vulnerable to a moderate Dutch Strategy if there are
This suggests the following sort of argument against someone who will update by something other than conditionalizing in the face of some evidence they might acquire. Suppose $c$ is your credence function at time $t$---it is defined on $\mathcal{F}$. There's some proposition $E$ in $\mathcal{F}$ that you might learn as evidence between an earlier time $t$ and a later time $t'$. And you'll learn $E$ just in case it's true. And suppose $c(E) > 0$. If you learn $E$---that is, if $E$ is true---you'll adopt credence function $c'$. If you don't learn $E$---that is, if $E$ is false---we don't know how you'll respond---perhaps it isn't determined. Then we'll say that you are vulnerable to a moderate Dutch Strategy if there are
- bets $B$ that $c$ requires you to accept,
- bets $B'_E$ that $c'$ requires you to accept, and
- bets $B'_{\overline{E}}$ that any credence function requires you to accept
such that
- the bets in $B$ and $B'_E$, taken together, lose you money in all worlds at which $E$ is true, and
- the bets in $B$ and $B'_{\overline{E}}$, taken together, lose you money in all worlds at which $E$ is false.
And we'll say that you are irrational if you are vulnerable to a moderate Dutch Strategy. Now, if we accept this, we can give an argument for updating by conditionalizing that appeals to sure loss bets. Following R. A. Briggs' presentation of David Lewis' argument, here's how (Lewis 1999, Briggs 2009).
Suppose $c'(X) = r' < r = c(X|E)$ and $c(E) = d > 0$. Then let $0 < \varepsilon < \frac{d(r-r')}{3}$. Then it is easy to see that your credences require you to accept the following bets:
Suppose $c'(X) = r' < r = c(X|E)$ and $c(E) = d > 0$. Then let $0 < \varepsilon < \frac{d(r-r')}{3}$. Then it is easy to see that your credences require you to accept the following bets:
After all, Bets 1 and 2 have positive expected value relative to $c$, and Bet 3 has positive expected value relative to $c'$, which you will adopt at $t'$ if $E$ is true. And it is easy to calculate that, if $E$ is true, then Bets 1, 2, and 3 taken together lose you money; and if $E$ is false, then Bets 1 and 2 taken together lose you money.
Now notice that this argument is directed against someone who will update by something other than conditionalization on certain evidence she might receive. Thus, at least on the face of it, it is not directed against Sandy's actual updating behaviour, but rather against his dispositions to update in different ways depending on the evidence he receives---what we might call his updating rule. That is, the object of criticism against which the Dutch Strategy argument is posed is Sandy's updating rule. One way to see this is to ask what would happen if Sandy instead learned $\overline{E}$ and updated on $\overline{E}$ by conditionalizing on it. Then, even though his actual updating behaviour would have been in line with Actual Conditionalization, he would nonetheless still have been vulnerable to a Dutch Strategy because he would have strayed from conditionalization had he learned $E$ instead. This shows that Dutch Strategy arguments target irreducibly modal features of an agent---that is, they target rules or dispositions, not actual behaviour. We will see this again below. Thus, we might take the Dutch Strategy argument to establish the following norm, at least in the first instance:
Now notice that this argument is directed against someone who will update by something other than conditionalization on certain evidence she might receive. Thus, at least on the face of it, it is not directed against Sandy's actual updating behaviour, but rather against his dispositions to update in different ways depending on the evidence he receives---what we might call his updating rule. That is, the object of criticism against which the Dutch Strategy argument is posed is Sandy's updating rule. One way to see this is to ask what would happen if Sandy instead learned $\overline{E}$ and updated on $\overline{E}$ by conditionalizing on it. Then, even though his actual updating behaviour would have been in line with Actual Conditionalization, he would nonetheless still have been vulnerable to a Dutch Strategy because he would have strayed from conditionalization had he learned $E$ instead. This shows that Dutch Strategy arguments target irreducibly modal features of an agent---that is, they target rules or dispositions, not actual behaviour. We will see this again below. Thus, we might take the Dutch Strategy argument to establish the following norm, at least in the first instance:
Rule Conditionalization If
- $c$ is your credence function at $t$,
- if $E$ is the strongest evidence you obtain between $t$ and $t'$, then you will adopt $c'$ as your credence function at $t'$,
- $c(E) > 0$,
then it ought to be that $c'(X) = c(X|E)$, for all $X$.
The crucial difference between Actual and Rule Conditionalization lies in the modal status of the second clause. Whereas Actual Conditionalization targets what you actually have done, Rule Conditionalization targets what you will do.
Now, it might seem that we can salvage an argument for Actual Conditionalization from Rule Conditionalization. Sandy violates Actual Conditionalization because his unconditional credence in $M$ on Tuesday is 70% while his conditional credence in $M$ given $E$ on Monday is 60%. But surely it is then true on Monday that he will adopt a credence of 70% in $M$ on Tuesday if he learns $E$. That is, he violates Rule Conditionalization as well.
But there is a problem with that reasoning. Suppose Sandy's credences don't evolve deterministically. That is, suppose that, while on Tuesday it turns out that he in fact responded to learning $E$ by raising his confidence in $M$ to 70%, he might have responded differently. For instance, suppose that there was some possibility that he responded to the evidence $E$ by dropping his confidence to 50%. Then the Dutch strategy against Sandy described above has a hole. It tells us what to do if he learns $E$ and responds by becoming 70% confident in $M$. And it tells us what to do if he learns $\overline{E}$. But it says nothing about what to do if he learns $E$ and he drops his confidence in $M$ to 50%. And indeed it turns out that it isn't always possible to fill that gap. Thus, what the standard Dutch Strategy argument sketched above shows is that there always a Dutch strategy against someone with a deterministic update rule that would make them stray from conditionalizing in some cases. Now, it turns out that, for certain non-deterministic updating rules, we can create Dutch Strategies against them too. But not all of them. Indeed, there are non-deterministic ways to update your credences that always lead you to not conditionalize, but for which there is no strategy for creating a Dutch Book against you.
I'll illustrate this with an example first, and then I'll state the central fact of which the example is a particular case. Suppose Sandy does not update by a purely deterministic rule. Rather, his credences develop as depicted in Figure 1.
The crucial difference between Actual and Rule Conditionalization lies in the modal status of the second clause. Whereas Actual Conditionalization targets what you actually have done, Rule Conditionalization targets what you will do.
Now, it might seem that we can salvage an argument for Actual Conditionalization from Rule Conditionalization. Sandy violates Actual Conditionalization because his unconditional credence in $M$ on Tuesday is 70% while his conditional credence in $M$ given $E$ on Monday is 60%. But surely it is then true on Monday that he will adopt a credence of 70% in $M$ on Tuesday if he learns $E$. That is, he violates Rule Conditionalization as well.
But there is a problem with that reasoning. Suppose Sandy's credences don't evolve deterministically. That is, suppose that, while on Tuesday it turns out that he in fact responded to learning $E$ by raising his confidence in $M$ to 70%, he might have responded differently. For instance, suppose that there was some possibility that he responded to the evidence $E$ by dropping his confidence to 50%. Then the Dutch strategy against Sandy described above has a hole. It tells us what to do if he learns $E$ and responds by becoming 70% confident in $M$. And it tells us what to do if he learns $\overline{E}$. But it says nothing about what to do if he learns $E$ and he drops his confidence in $M$ to 50%. And indeed it turns out that it isn't always possible to fill that gap. Thus, what the standard Dutch Strategy argument sketched above shows is that there always a Dutch strategy against someone with a deterministic update rule that would make them stray from conditionalizing in some cases. Now, it turns out that, for certain non-deterministic updating rules, we can create Dutch Strategies against them too. But not all of them. Indeed, there are non-deterministic ways to update your credences that always lead you to not conditionalize, but for which there is no strategy for creating a Dutch Book against you.
I'll illustrate this with an example first, and then I'll state the central fact of which the example is a particular case. Suppose Sandy does not update by a purely deterministic rule. Rather, his credences develop as depicted in Figure 1.
Thus, whatever happens, Sandy will not update by conditionalizing. However, there is no Dutch strategy against him. The reason is that, while Sandy does not update by conditionalizing on his strongest evidence on Tuesday, there is a way of representing him as if he were updating by conditionalization on some evidence, namely, the identity of his credence function on Tuesday. First, notice that Sandy's credence function $c$ on Monday is the average of the possible credence functions he might adopt on Tuesday---that is, for any $X$ in $\mathcal{F}$,
$$c(X) = \frac{1}{4}c_1(X) + \frac{1}{4}c_2(X) + \frac{1}{4}c_3(X) + \frac{1}{4}c_4(X)$$
Now, suppose we expand the set of propositions $\mathcal{F}$ to which Sandy assigns credences by adding, for each possible future credence function $c_i$, the proposition $C_{c_i}$, which says that $c_i$ is Sandy's credence function on Tuesday. And then suppose we extend $c$ to $c^*$, which is defined on this expanded set of propositions as follows: given a possible world $w$, let
\[
c^*(w\ \&\ C_{c_i}) = \frac{1}{4}c_i(w)
\]
Then it's easy to verify that $c^*(X) = c(X)$ for any $X$ in $\mathcal{F}$. So $c^*$ really is an extension of $c$. And we can also see that
\[
c^*(M | C_{c_i}) = \frac{c^*(M\ \&\ C_{c_i})}{c^*(C_{c_i})} = \frac{\frac{1}{4}c_i(M)}{\frac{1}{4}} = c_i(M)
\]
So, $c_i$ is the result of conditionalizing $c^*$ on the proposition that $c_i$ is Sandy's credence function on Tuesday. As we see in Theorem 1 below, there can be no Dutch Strategy against Sandy because he can be represented as if he is updating on these propositions about his Tuesday credences, even though that is not in fact how his updating proceeds. This shows again that whatever sure loss argument we have for updating, it does not target actual updating, but rather updating rules or dispositions. For it is possible to have an update rule that makes it certain that you will violate Actual Conditionalization, and yet not be vulnerable to a Dutch Strategy.
Before we state our theorem, some terminology: Suppose $c$ is your credence function at $t$. It is defined on a set of propositions $\mathcal{F}$. Suppose $\mathcal{E} = \{E_1, \ldots, E_n\} \subseteq \mathcal{F}$ is a partition that contains the strongest propositions you might learn between $t$ and $t'$. Suppose $\mathcal{C} = \{c_1, \ldots, c_m\}$ is the set of possible credence functions you might adopt at $t'$. They are also defined on $\mathcal{F}$. So:
Now, suppose we expand the set of propositions $\mathcal{F}$ to which Sandy assigns credences by adding, for each possible future credence function $c_i$, the proposition $C_{c_i}$, which says that $c_i$ is Sandy's credence function on Tuesday. And then suppose we extend $c$ to $c^*$, which is defined on this expanded set of propositions as follows: given a possible world $w$, let
\[
c^*(w\ \&\ C_{c_i}) = \frac{1}{4}c_i(w)
\]
Then it's easy to verify that $c^*(X) = c(X)$ for any $X$ in $\mathcal{F}$. So $c^*$ really is an extension of $c$. And we can also see that
\[
c^*(M | C_{c_i}) = \frac{c^*(M\ \&\ C_{c_i})}{c^*(C_{c_i})} = \frac{\frac{1}{4}c_i(M)}{\frac{1}{4}} = c_i(M)
\]
So, $c_i$ is the result of conditionalizing $c^*$ on the proposition that $c_i$ is Sandy's credence function on Tuesday. As we see in Theorem 1 below, there can be no Dutch Strategy against Sandy because he can be represented as if he is updating on these propositions about his Tuesday credences, even though that is not in fact how his updating proceeds. This shows again that whatever sure loss argument we have for updating, it does not target actual updating, but rather updating rules or dispositions. For it is possible to have an update rule that makes it certain that you will violate Actual Conditionalization, and yet not be vulnerable to a Dutch Strategy.
Before we state our theorem, some terminology: Suppose $c$ is your credence function at $t$. It is defined on a set of propositions $\mathcal{F}$. Suppose $\mathcal{E} = \{E_1, \ldots, E_n\} \subseteq \mathcal{F}$ is a partition that contains the strongest propositions you might learn between $t$ and $t'$. Suppose $\mathcal{C} = \{c_1, \ldots, c_m\}$ is the set of possible credence functions you might adopt at $t'$. They are also defined on $\mathcal{F}$. So:
- for each $E_i$ in $\mathcal{E}$, there is at least one $c_j$ in $\mathcal{C}$ such that $c_j(E_i) = 1$---that is, for every possible piece of evidence you might acquire, there is some possible future credence function that is a response to that evidence;
- for each $c_j$ in $\mathcal{C}$, there is exactly one $E_i$ in $\mathcal{E}$ such that $c_j(E_i) = 1$---that is, every possible future credence function is a response to exactly one of these possible pieces of evidence.
Then we say that there is a strong Dutch Strategy against you iff there are sets of bets $B$ and $B'$ such that
- $c$ requires you to accept the bets in $B$,
- $c_j$ requires you to accept the bets in $B'$, for all $1 \leq j \leq m$, and
- taken together, the bets in $B$ and $B'$ lose you money in all epistemically possible worlds.
And we say that there is a weak Dutch Strategy against you iff there are sets of bets $B, B'_1, \ldots, B'_n$ such that
- $c$ requires you to accept the bets in $B$,
- $c_j$ requires you to accept the bets in $B'_j$, for all $1 \leq j \leq m$, and
- the bets in $B$ and $B_j$, taken together, lose you money at all worlds at which you have credence function $c_j$ at time $t'$.
Note: if you are vulnerable to a strong Dutch Strategy, you're certainly vulnerable to a weak Dutch Strategy; if you are not vulnerable to a weak Dutch Strategy, then you cannot be vulnerable to a strong Dutch Strategy.
We say that you are representable as a conditionalizer iff there is an extension of $c, c_1, \ldots, c_m$ to credence functions $c^*, c^*_1, \ldots, c^*_m$ defined on $(\mathcal{F} \cup \{C_{c_1}, \ldots, C_{c_m}\})^*$ such that
We say that you are representable as a conditionalizer iff there is an extension of $c, c_1, \ldots, c_m$ to credence functions $c^*, c^*_1, \ldots, c^*_m$ defined on $(\mathcal{F} \cup \{C_{c_1}, \ldots, C_{c_m}\})^*$ such that
- $c^*_i(C_{c_i}) = 1$, for $1 \leq i \leq m$;
- $c^*_i(X) = c^*(X | C_{c_i})$ for $X$ in $(\mathcal{F} \cup \{C_{c_1}, \ldots, C_{c_m}\})^*$
Theorem 1
- If you are not representable as a conditionalizer, there is a strong Dutch Strategy against you;
- If you are representable as a conditionalizer, there is no weak (or strong) Dutch Strategy against you.
I won't give the full proof here, but it runs roughly as follows: you are representable as a conditionalizer iff $c$ is in the convex hull of $\{c_1, \ldots, c_n\}$ and if $c$ is not in the convex hull of $\{c_1, \ldots, c_n\}$, then there is a set of bets that $c$ requires you to buy for one price, while each $c_i$ requires you to sell them for a lower price.
Now, suppose your updating rule is deterministic. Then, for each $E_i$, there is exactly one $c_j$ in $\mathcal{C}$ such that $c_j(E_i) = 1$. Thus, in this case, your updating rule is vulnerable to a strong Dutch Strategy if it is not a conditionalizing rule, and not vulnerable even to a weak Dutch Strategy if it is. Thus, we have an extra argument for Rule Conditionalization. In some ways it strengthens the standard argument presented above, for it shows that the same set of bets can be offered at $t'$ regardless of what credence function you end up having. But in some ways it weakens that argument, for it relies on the assumption that there is a finite set of possible future credence functions you might adopt at $t'$.
Now, of course, you might object that updating other than by a deterministic rule is irrational: your evidence, together with your prior credences, should determine your new credences; there should not be many possible ways you might respond to the same piece of evidence. This may be true, and if we supplement the Dutch Strategy argument with this assumption, we obtain a Dutch Strategy for conditionalizing. But note that the argument is no longer purely pragmatic. It is now partly evidentialist, because it incorporates this evidentialist principle that we have not and cannot justify on pragmatic grounds---we cannot specify how you will go wrong in your decisions if you update using a non-deterministic rule.
Now, of course, you might object that updating other than by a deterministic rule is irrational: your evidence, together with your prior credences, should determine your new credences; there should not be many possible ways you might respond to the same piece of evidence. This may be true, and if we supplement the Dutch Strategy argument with this assumption, we obtain a Dutch Strategy for conditionalizing. But note that the argument is no longer purely pragmatic. It is now partly evidentialist, because it incorporates this evidentialist principle that we have not and cannot justify on pragmatic grounds---we cannot specify how you will go wrong in your decisions if you update using a non-deterministic rule.
References
- Briggs, R. A. (2009). Distorted Reflection. Philosophical Review, 118(1), 59–85.
- Lewis, D. (1999). Why Conditionalize? In Papers in Metaphysics and Epistemology. Cambridge, UK: Cambridge University Press.
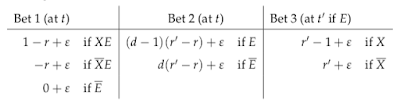


This comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteUseful article, thank you for sharing the article!!!
ReplyDeleteWebsite bloggiaidap247.com và website blogcothebanchuabiet.com giúp bạn giải đáp mọi thắc mắc.
Seorang Bill Gates memiliki beberapa opsi untuk menilai kesuksesan yakni harus diukur dari perubahan dan revolusi. Hal ini telah banyak membuahkan inspirasi bagi pebisnis dan juga para inovator. https://mencariuang.web.id Sehingga ada sejumlah poin berbeda-beda yang kemudian bisa langsung dicermati sebagai modal dasar untuk mengembangkan diri dan juga disesuaikan dengan beberapa prospek di dalam kehidupan.
ReplyDelete