Updating by minimizing expected inaccuracy -- or: my new favourite scoring rule
For a PDF version of this post, click here.
One of the central questions of Bayesian epistemology concerns how you should update your credences in response to new evidence you obtain. The proposal I want to discuss here belongs to an approach that consists of two steps. First, we specify the constraints that your evidence places on your posterior credences. Second, we specify a means by which to survey the credence functions that satisfy those constraints and pick one to adopt as your posterior.
For instance, in the first step, we might say that when we learn a proposition $E$, we must become certain of it, and so it imposes the following constraint on our posterior credence function $Q$: $Q(E) = 1$. Or we might consider the sort of situation Richard Jeffrey discussed, where there is a partition $E_1, \ldots, E_m$ and credences $q_1, \ldots, q_m$ with $q_1 + \ldots + q_m = 1$ such that your evidence imposes the constraint: $Q(E_i) = q_i$, for $i = 1, \ldots, m$. Or the situation van Fraassen discussed, where your evidence constrains your posterior conditional credences, so that there is a credence $q$ and propositions $A$ and $B$ such that your evidence imposes the constraint: $Q(A|B) = q$.
In the second step of the approach, on the other hand, we might following objective Bayesians like Jon Williamson, Alena Vencovská, and Jeff Paris and say that, from among those credence functions that respect your evidence, you should pick the one that, on a natural measure of informational content, contains minimal information, and which thus goes beyond your evidence as little as possible (Paris & Vencovská 1990, Williamson 2010). Or we might follow what I call the method of minimal mutilation proposed by Persi Diaconis and Sandy Zabell and pick the credence function among those that respect the evidence that is closest to your prior according to some measure of divergence between probability functions (Diaconis & Zabell 1982). Or, you might proceed as Hannes Leitgeb and I suggested and pick the credence function that minimizes expected inaccuracy from the point of view of your prior, while satisfying the constraints the evidence imposes (Leitgeb & Pettigrew 2010). In this post, I'd like to fix a problem with the latter proposal.
We'll focus on the simplest case: you learn $E$ and this requires you to adopt a posterior $Q$ such that $Q(E) = 1$. This is also the case in which the norm governing it is least controversial. The largely undisputed norm in this case says that you should conditionalize your prior on your evidence, so that, if $P$ is your prior and $P(E) > 0$, then your posterior should be $Q(-) = P(-|E)$. That is, providing you assigned a positive credence to $E$ before you learned it, your credence in the proposition $X$ after learning $E$ should be your prior credence in $X$ conditional on $E$.
In order to make the maths as simple as possible, let's assume you assign credences to a finite set of worlds $\{w_1, \ldots, w_n\}$, which forms a partition of logical space. Given a credence function $P$, we write $p_i$ for $P(w_i)$, and we'll sometimes represent $P$ by the vector $(p_1, \ldots, p_n)$. Let's suppose further that your measure of the inaccuracy of a credence function is $\mathfrak{I}$, which is generated additively from a scoring rule $\mathfrak{s}$. That is,
$$ \mathrm{Exp}_\mathfrak{I}(Q | P) = \sum^n_{i=1} p_i \mathfrak{I}(Q, w_i)$$
At this point, however, a problem arises. There are two inaccuracy measures that tend to be used in statistics and accuracy-first epistemology. The first is the Brier inaccuracy measure $\mathfrak{B}$, which is generated by the quadratic scoring rule $\mathfrak{q}$:
$$\mathfrak{q}_0(x) = x^2\ \ \ \mbox{and}\ \ \ \ \mathfrak{q}_1(x) = (1-x)^2$$
So
$$\mathfrak{B}(P, w_i) = 1-2p_i + \sum^n_{i=1} p_i^2$$
The second is the local log inaccuracy measure $\mathfrak{L}$, which is generated by what I'll call here the basic log score $\mathfrak{l}$:
$$\mathfrak{l}_0(x) = 0\ \ \ \ \mbox{and}\ \ \ \ \mathfrak{l}_1(x) = -\log x$$
So
$$\mathfrak{L}(P, w_i) = -\log p_i$$
The problem is that both have undesirable features for this purpose: the Brier inaccuracy measure does not deliver Conditionalization when you take the approach Hannes and I described; the local log inaccuracy measure does give Conditionalization, but while it is strictly proper in a weak sense, the basic log score that generates it is not; and relatedly, but more importantly, the local log inaccuracy measure does not furnish an accuracy dominance argument for Probabilism. Let's work through this in more detail.
According to the standard Bayesian norm of Conditionalization, if $P$ is your prior and $P(E) > 0$, then your posterior after learning at most $E$ should be $Q(-) = P(-|E)$. That is, when I remove all credence from the worlds at which my evidence is false, in order to respect my new evidence, I should redistribute it to the worlds at which my evidence is true in proportion to my prior credence in those worlds.
Now suppose that I update instead by picking the posterior $Q$ for which $Q(E) = 1$ and that minimizes expected inaccuracy as measured by the Brier inaccuracy measure. Then, at least in most cases, when I remove all credence from the worlds at which my evidence is false, in order to respect my new evidence, I redistribute it equally to the worlds at which my evidence is true---not in proportion to my prior credence in those worlds, but equally to each, regardless of my prior attitude.
Here's a quick illustration in the case in which you distribute your credences over three worlds, $w_1$, $w_2$, $w_3$ and the proposition you learn is $E = \{w_1, w_2\}$. Then we want to find a posterior $Q = (x, 1-x, 0)$ with minimal expected Brier inaccuracy from the point of view of the prior $P = (p_1, p_2, p_3)$. Then:
\begin{eqnarray*}
& & \mathrm{Exp}_\mathfrak{B}((x, 1-x, 0) | (p_1, p_2, p_3))\\
& = & p_1[(1-x)^2 + (1-x)^2 + 0^2] + p_2[x^2 + x^2 + 0^2] +p_3[x_2 + (1-x)^2 + 1]
\end{eqnarray*}
Differentiating this with respect to $x$ gives $$-4p_1 + 4x - 2p_3$$ which equals 0 iff $$x = p_1 + \frac{p_3}{3}$$ Thus, providing $p_1 + \frac{p_3}{3}, p_2 + \frac{p_3}{3} \leq 1$, then the posterior that minimizes expected Brier inaccuracy while respecting the evidence is $$Q = \left (p_1 + \frac{p_3}{3}, p_2 + \frac{p_3}{3}, 0 \right )$$ And this is typically not the same as Conditionalization demands.
Now turn to the local log measure, $\mathfrak{L}$. Here, things are actually a little complicated by the fact that $-\log 0 = \infty$. After all, $$\mathrm{Exp}_\mathfrak{L}((x, 1-x, 0)|(p_1, p_2, p_3)) = -p_1\log x - p_2 \log (1-x) - p_3 \log 0$$ and this is $\infty$ regardless of the value of $x$. So every value of $x$ minimizes, and indeed maximizes, this expectation. As a result, we have to look at the situation in which the evidence imposes the constraint $Q(E) = 1-\varepsilon$ for $\varepsilon > 0$, and ask what happens as we let $\varepsilon$ approach 0. Then
$$\mathrm{Exp}_\mathfrak{L}((x, 1-\varepsilon-x, \varepsilon)|(p_1, p_2, p_3)) = -p_1\log x - p_2 \log (1-\varepsilon-x) - p_3 \log \varepsilon$$
Differentiating this with respect to $x$ gives
$$-\frac{p_1}{x} + \frac{p_2}{1-\varepsilon - x}$$
which equals 0 iff
$$x = (1-\varepsilon) \frac{p_1}{p_1 + p_2}$$
And this approaches Conditionalization as $\varepsilon$ approaches 0. So, in this sense, as Ben Levinstein pointed out, the local log inaccuracy measure gives Conditionalization, and indeed Jeffrey Conditionalization or Probability Kinematics as well (Levinstein 2012). So far, so good.
However, throughout this post, and in the two derivations above---the first concerning the Brier inaccuracy measure and the second concerning the local log inaccuracy measure---we assumed that all credence functions must be probability functions. That is, we assumed Probabilism, the other central tenet of Bayesianism alongside Conditionalization. Now, if we measure inaccuracy using the Brier measure, we can justify that, for then we have the accuracy dominance argument, which originated mathematically with Bruno de Finetti, and was given its accuracy-theoretic philosophical spin by Jim Joyce (de Finetti 1974, Joyce 1998). That is, if your prior or your posterior isn't a probability function, then there is an alternative that is and that is guaranteed to be more Brier-accurate. However, the local log inaccuracy measure doesn't furnish us with any such argument. One very easy way to see this is to note that the non-probabilistic credence function $(1, 1, \ldots, 1)$ over $\{w_1, \ldots, w_n\}$ dominates all other credence functions according to the local log measure. After all, $\mathfrak{L}((1, 1, \ldots, 1), w_i) = -\log 1 = 0$, for $i = 1, \ldots, n$, while $\mathfrak{L}(P, w_i) > 0$ for any $P$ with $p_i < 1$ for some $i = 1, \ldots, n$.
Another related issue is that the scoring rule $\mathfrak{l}$ that generates $\mathfrak{L}$ is not strictly proper. A scoring rule $\mathfrak{s}$ is said to be strictly proper if every credence expects itself to be the best. That is, for any $0 \leq p \leq 1$, $p\mathfrak{s}_1(x) + (1-p) \mathfrak{s}_0(x)$ is minimized, as a function of $x$, at $x = p$. But $-p\log x + (1-p)0 = -p\log x$ is always minimized, as a function of $x$, at $x = 1$, where $-p\log x = 0$. Similarly, an inaccuracy measure $\mathfrak{I}$ is strictly proper if, for any probabilistic credence function $P$, $\mathrm{Exp}_\mathfrak{I}(Q | P) = \sum^n_{i=1} p_i \mathfrak{I}(Q, w_i)$ is minimized, as a function of $Q$ at $Q = P$. Now, in this sense, $\mathfrak{L}$ is not strictly proper, since $\mathrm{Exp}_\mathfrak{L}(Q | P) = \sum^n_{i=1} p_i \mathfrak{L}(Q, w_i)$ is minimized, as function of $Q$ at $Q = (1, 1, \ldots, 1)$, as noted above. Nonetheless, if we restrict our attention to probabilistic $Q$, $\mathrm{Exp}_\mathfrak{L}(Q | P) = \sum^n_{i=1} p_i \mathfrak{L}(c, w_i)$ is minimized at $Q = P$. In sum: $\mathfrak{L}$ is only a reasonable inaccuracy measure to use if you already have an independent motivation for Probabilism. But accuracy-first epistemology does not have that luxury. One of central roles of an inaccuracy measure in that framework is to furnish an accuracy dominance argument for Probabilism.
So, we ask: is there a scoring rule $\mathfrak{s}$ and resulting inaccuracy measure $\mathfrak{I}$ such that:
$$\mathfrak{l}^\star_0(x) = x\ \ \ \ \mathrm{and}\ \ \ \ \mathfrak{l}^\star_1(x) = -\log x + x-1$$
Before we state and prove the theorem, there are some features of this scoring rule and its resulting inaccuracy measure that are worth noting. Juergen Landes has identified this scoring rule for a different purpose (Proposition 9.1, Landes 2015).
Proposition 1 $\mathfrak{l}^\star$ is strictly proper.
Proof. Suppose $0 \leq p \leq 1$. Then
$$\frac{d}{dx} p\mathfrak{l}^\star_1(x) + (1-p)\mathfrak{l}^\star_0(x) = \frac{d}{dx} p[-\log x + x] + (1-p)x = -\frac{p}{x} + 1 = 0$$ iff $p = x$. $\Box$
Proposition 2 If $P$ is non-probabilistic, then $P^\star = \left (\frac{p_1}{\sum_k p_k}, \ldots, \frac{p_n}{\sum_k p_k} \right )$ accuracy dominates $P = (p_1, \ldots, p_n)$.
Proof. $$\mathfrak{L}^\star(P^\star, w_i) = -\log\left ( \frac{p_i}{\sum_k p_k} \right ) + 1 = -\log p_i + \log\sum_k p_k + 1$$ and $$\mathfrak{L}^\star(P, w_i) = -\log p_i + \sum_k p_k$$ But $\log x + 1 \leq x$, for all $x> 0$, with equality iff $x = 1$. So, if $P$ is non-probabilistic, then $\sum_k p_k \neq 1$ and $$\mathfrak{L}^\star(P^\star, w_i) < \mathfrak{L}^\star(P, w_i)$$ for $i = 1, \ldots, n$. $\Box$
Proposition 3 If $P$ is probabilistic, $\mathfrak{L}^\star(P, w_i) = 1 + \mathfrak{L}(P, w_i)$.
Proof.
\begin{eqnarray*}
\mathfrak{L}^\star(P, w_i) & = & p_1 + \ldots + p_{i-1} + (-\log p_i + p_i ) + p_{i+1} + \ldots + p_n \\
& = & -\log p_i + 1 \\
& = & 1 + \mathfrak{L}(P, w_i)
\end{eqnarray*}
$\Box$
Corollary 1 If $P$, $Q$ are probabilistic, then
$$\mathrm{Exp}_{\mathfrak{L}^\star}(Q | P) = 1 + \mathrm{Exp}_\mathfrak{L}(Q | P)$$
Proof. By Proposition 3. $\Box$
Corollary 2 Suppose $E_1, \ldots, E_m$ is a partition and $0 \leq q_1, \ldots, q_m \leq 1$ with $\sum^m_{i=1} q_i = 1$. Then, among $Q$ for which $Q(E_i) = q_i$ for $i = 1, \ldots, m$, $\mathrm{Exp}_{\mathfrak{L}^\star}(Q |P)$ is minimized at the Jeffrey Conditionalization posterior $Q(-) = \sum^k_{i=1} q_iP(-|E_i)$.
Proof. This follows from Corollary 1 and Theorem 5.1 from (Diaconis & Zabell 1982). $\Box$
Having seen $\mathfrak{l}^\star$ and $\mathfrak{L}^\star$ in action, let's see that they are unique in having this combination of features.
Theorem 1 Suppose $\mathfrak{s}$ is a strictly proper scoring rule and $\mathfrak{I}$ is the inaccuracy measure it generates. And suppose that, for any $\{w_1, \ldots, w_n\}$ and any $E \subseteq \{w_1, \ldots, w_n\}$, and any probabilistic credence function $P$, the probabilistic credence function $Q$ that minimizes the expected inaccuracy of $Q$ with respect to $P$ with the constraint $Q(E) = 1$, and when inaccuracy is measured by $\mathfrak{I}$, is $Q(-) = P(-|E)$. Then the scoring rule is
$$\mathfrak{s}_1(x) = -\log x +x\ \ \ \ \mbox{and}\ \ \ \ \mathfrak{s}_0(x) = x$$ or any affine transformation of this.
Proof. First, we appeal to the following lemma (Proposition 2, Predd, et al. 2009):
Lemma 1
(i) Suppose $\mathfrak{s}$ is a continuous strictly proper scoring rule. Then define$$\varphi_\mathfrak{s}(x) = -x\mathfrak{s}_1(x) - (1-x)\mathfrak{s}_0(x)$$Then $\varphi_\mathfrak{s}$ is differentiable on $(0, 1)$ and convex on $[0, 1]$ and $$\mathrm{Exp}_\mathfrak{I}(Q | P) - \mathrm{Exp}_\mathfrak{I}(P | P) = \sum^n_{i=1} \varphi_\mathfrak{s}(p_i) - \varphi_\mathfrak{s}(q_i) - \varphi_\mathfrak{s}^\prime (q_i)(p_i - q_i)$$ (ii) Suppose $\varphi$ is differentiable on $(0, 1)$ and convex on $[0, 1]$. Then let
Moreover, $\mathfrak{s}^{\varphi_\mathfrak{s}} = \mathfrak{s}$.
Now, let's focus on $\{w_1, w_2, w_3, w_4\}$ and let $E = \{w_1, w_2, w_3\}$. Let $p_1 = a$, $p_2 = b$, $p_3 = c$. Then we wish to minimize
$$\mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c))$$
Now, but Lemma 1,
\begin{eqnarray*}
&& \mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c)) \\
& = & \varphi(a) - \varphi(x) - \varphi'(x)(a-x)\\
& + & \varphi(b) - \varphi(y) - \varphi'(y)(b-y) \\
& + & \varphi(c) - \varphi(1-x-y) - \varphi'(1-x-y)(c - (1-x-y)) \\
& + & \mathrm{Exp}_\mathfrak{I}((a, b, c, 1-a-b-c) | (a, b, c, 1-a-b-c))
\end{eqnarray*}
Thus:
\begin{eqnarray*}
&& \frac{\partial}{\partial x} \mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c))\\
& = & \varphi''(x)(x-a) - ((1-x-y) - c) \varphi''(1-x-y)
\end{eqnarray*}
and
\begin{eqnarray*}
&& \frac{\partial}{\partial y} \mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c))\\
& = & \varphi''(y)(y-b) - ((1-x-y) - c) \varphi''(1-x-y)
\end{eqnarray*}
which are both 0 iff$$\varphi''(x)(x-a) = \varphi''(y)(y-b) = ((1-x-y) - c) \varphi''(1-x-y)$$ Now, suppose this is true for $x = \frac{a}{a+b+c}$ and $y = \frac{b}{a + b+ c}$. Then, for all $0 \leq a, b, c \leq 1$ with $a + b + c \leq 1$, $$a\varphi'' \left ( \frac{a}{a+b+c} \right ) = b\varphi'' \left ( \frac{b}{a+b+c} \right ) $$
We now wish to show that $\varphi''(x) = \frac{k}{x}$ for all $0 \leq x \leq 1$. If we manage that, then it follows that $\varphi'(x) = k\log x + m$ and $\varphi(x) = kx\log x + (m-k)x$. And we know from Lemma 1:
\begin{eqnarray*}
& & \mathfrak{s}_0(x) \\
& = & - \varphi(x) - \varphi'(x)(0-x) \\
& = & - [kx\log x + (m-k)x] - [k\log x + m](0-x) \\
& = & kx
\end{eqnarray*}
and
\begin{eqnarray*}
&& \mathfrak{s}_1(x) \\
& = & - \varphi(x) - \varphi'(x)(1-x) \\
& = & - [kx\log x + (m-k)x] - [k\log x + m](1-x) \\
& = & -k\log x + kx - m
\end{eqnarray*}
Now, first, let $f(x) = \varphi''\left (\frac{1}{x} \right )$. Thus, it will suffice to prove that $f(x) = x$. For then $\varphi''(x) = \varphi''\left (\frac{1}{\frac{1}{x}} \right ) = f \left ( \frac{1}{x} \right ) = \frac{1}{x}$, as required. And to prove $f(x) = x$, we need only show that $f'(x)$ is a constant function. We know that, for all $0 \leq a, b, c \leq 1$ with $a + b + c \leq 1$, we have
$$a f \left ( \frac{a + b + c}{a} \right ) = bf \left ( \frac{a + b + c}{b} \right )$$
So$$
\frac{d}{dx} a f \left ( \frac{a + b + x}{a} \right ) = \frac{d}{dx} bf \left ( \frac{a + b + x}{b} \right )
$$So, for all $0 \leq a, b, c \leq 1$ with $a + b + c \leq 1$
$$
f'\left (\frac{a+b+c}{a} \right ) = f'\left (\frac{a + b + c}{b} \right )
$$We now show that, for all $x \geq 1$, $f'(x) = f'(2)$, which will suffice to show that it is constant. First, we consider $2 \leq x$. Then let
$$a = \frac{1}{x}\ \ \ \ \ b = \frac{1}{2}\ \ \ \ \ c = \frac{1}{2}-\frac{1}{x}$$
Then
$$f'(x) = f'\left (\frac{a + b + c}{a} \right ) = f'\left (\frac{a + b + c}{b} \right ) = f'(2)$$
Second, consider $1 \leq x \leq 2$. Then pick $2 \leq y$ such that $\frac{1}{x} + \frac{1}{y} \leq 1$. Then let
$$a = \frac{1}{x}\ \ \ \ \ b = \frac{1}{y}\ \ \ \ \ c = 1 - \frac{1}{x} - \frac{1}{y}$$
Then
$$f'(x) = f'\left (\frac{a + b + c}{a} \right ) = f'\left (\frac{a + b + c}{b} \right ) = f'(y) = f'(2)$$
as required. $\Box$
One of the central questions of Bayesian epistemology concerns how you should update your credences in response to new evidence you obtain. The proposal I want to discuss here belongs to an approach that consists of two steps. First, we specify the constraints that your evidence places on your posterior credences. Second, we specify a means by which to survey the credence functions that satisfy those constraints and pick one to adopt as your posterior.
For instance, in the first step, we might say that when we learn a proposition $E$, we must become certain of it, and so it imposes the following constraint on our posterior credence function $Q$: $Q(E) = 1$. Or we might consider the sort of situation Richard Jeffrey discussed, where there is a partition $E_1, \ldots, E_m$ and credences $q_1, \ldots, q_m$ with $q_1 + \ldots + q_m = 1$ such that your evidence imposes the constraint: $Q(E_i) = q_i$, for $i = 1, \ldots, m$. Or the situation van Fraassen discussed, where your evidence constrains your posterior conditional credences, so that there is a credence $q$ and propositions $A$ and $B$ such that your evidence imposes the constraint: $Q(A|B) = q$.
In the second step of the approach, on the other hand, we might following objective Bayesians like Jon Williamson, Alena Vencovská, and Jeff Paris and say that, from among those credence functions that respect your evidence, you should pick the one that, on a natural measure of informational content, contains minimal information, and which thus goes beyond your evidence as little as possible (Paris & Vencovská 1990, Williamson 2010). Or we might follow what I call the method of minimal mutilation proposed by Persi Diaconis and Sandy Zabell and pick the credence function among those that respect the evidence that is closest to your prior according to some measure of divergence between probability functions (Diaconis & Zabell 1982). Or, you might proceed as Hannes Leitgeb and I suggested and pick the credence function that minimizes expected inaccuracy from the point of view of your prior, while satisfying the constraints the evidence imposes (Leitgeb & Pettigrew 2010). In this post, I'd like to fix a problem with the latter proposal.
We'll focus on the simplest case: you learn $E$ and this requires you to adopt a posterior $Q$ such that $Q(E) = 1$. This is also the case in which the norm governing it is least controversial. The largely undisputed norm in this case says that you should conditionalize your prior on your evidence, so that, if $P$ is your prior and $P(E) > 0$, then your posterior should be $Q(-) = P(-|E)$. That is, providing you assigned a positive credence to $E$ before you learned it, your credence in the proposition $X$ after learning $E$ should be your prior credence in $X$ conditional on $E$.
In order to make the maths as simple as possible, let's assume you assign credences to a finite set of worlds $\{w_1, \ldots, w_n\}$, which forms a partition of logical space. Given a credence function $P$, we write $p_i$ for $P(w_i)$, and we'll sometimes represent $P$ by the vector $(p_1, \ldots, p_n)$. Let's suppose further that your measure of the inaccuracy of a credence function is $\mathfrak{I}$, which is generated additively from a scoring rule $\mathfrak{s}$. That is,
- $\mathfrak{s}_1(x)$ measures the inaccuracy of credence $x$ in a truth;
- $\mathfrak{s}_0(x)$ measures the inaccuracy of credence $x$ in a falsehood;
- $\mathfrak{I}(P, w_i) = \mathfrak{s}_0(p_1) + \mathfrak{s}_0(p_{i-1} ) + \mathfrak{s}_1(p_i) + \mathfrak{s}_0(p_{i+1} ) + \ldots + \mathfrak{s}_0(p_n)$.
- $Q(E) = 1$;
- for any other credence function $Q^\star$ for which $Q^\star(E) = 1$, the expected inaccuracy of $Q$ by the lights of $P$ is less than the expected inaccuracy of $Q^\star$ by the lights of $P$.
$$ \mathrm{Exp}_\mathfrak{I}(Q | P) = \sum^n_{i=1} p_i \mathfrak{I}(Q, w_i)$$
At this point, however, a problem arises. There are two inaccuracy measures that tend to be used in statistics and accuracy-first epistemology. The first is the Brier inaccuracy measure $\mathfrak{B}$, which is generated by the quadratic scoring rule $\mathfrak{q}$:
$$\mathfrak{q}_0(x) = x^2\ \ \ \mbox{and}\ \ \ \ \mathfrak{q}_1(x) = (1-x)^2$$
So
$$\mathfrak{B}(P, w_i) = 1-2p_i + \sum^n_{i=1} p_i^2$$
The second is the local log inaccuracy measure $\mathfrak{L}$, which is generated by what I'll call here the basic log score $\mathfrak{l}$:
$$\mathfrak{l}_0(x) = 0\ \ \ \ \mbox{and}\ \ \ \ \mathfrak{l}_1(x) = -\log x$$
So
$$\mathfrak{L}(P, w_i) = -\log p_i$$
The problem is that both have undesirable features for this purpose: the Brier inaccuracy measure does not deliver Conditionalization when you take the approach Hannes and I described; the local log inaccuracy measure does give Conditionalization, but while it is strictly proper in a weak sense, the basic log score that generates it is not; and relatedly, but more importantly, the local log inaccuracy measure does not furnish an accuracy dominance argument for Probabilism. Let's work through this in more detail.
According to the standard Bayesian norm of Conditionalization, if $P$ is your prior and $P(E) > 0$, then your posterior after learning at most $E$ should be $Q(-) = P(-|E)$. That is, when I remove all credence from the worlds at which my evidence is false, in order to respect my new evidence, I should redistribute it to the worlds at which my evidence is true in proportion to my prior credence in those worlds.
Now suppose that I update instead by picking the posterior $Q$ for which $Q(E) = 1$ and that minimizes expected inaccuracy as measured by the Brier inaccuracy measure. Then, at least in most cases, when I remove all credence from the worlds at which my evidence is false, in order to respect my new evidence, I redistribute it equally to the worlds at which my evidence is true---not in proportion to my prior credence in those worlds, but equally to each, regardless of my prior attitude.
Here's a quick illustration in the case in which you distribute your credences over three worlds, $w_1$, $w_2$, $w_3$ and the proposition you learn is $E = \{w_1, w_2\}$. Then we want to find a posterior $Q = (x, 1-x, 0)$ with minimal expected Brier inaccuracy from the point of view of the prior $P = (p_1, p_2, p_3)$. Then:
\begin{eqnarray*}
& & \mathrm{Exp}_\mathfrak{B}((x, 1-x, 0) | (p_1, p_2, p_3))\\
& = & p_1[(1-x)^2 + (1-x)^2 + 0^2] + p_2[x^2 + x^2 + 0^2] +p_3[x_2 + (1-x)^2 + 1]
\end{eqnarray*}
Differentiating this with respect to $x$ gives $$-4p_1 + 4x - 2p_3$$ which equals 0 iff $$x = p_1 + \frac{p_3}{3}$$ Thus, providing $p_1 + \frac{p_3}{3}, p_2 + \frac{p_3}{3} \leq 1$, then the posterior that minimizes expected Brier inaccuracy while respecting the evidence is $$Q = \left (p_1 + \frac{p_3}{3}, p_2 + \frac{p_3}{3}, 0 \right )$$ And this is typically not the same as Conditionalization demands.
Now turn to the local log measure, $\mathfrak{L}$. Here, things are actually a little complicated by the fact that $-\log 0 = \infty$. After all, $$\mathrm{Exp}_\mathfrak{L}((x, 1-x, 0)|(p_1, p_2, p_3)) = -p_1\log x - p_2 \log (1-x) - p_3 \log 0$$ and this is $\infty$ regardless of the value of $x$. So every value of $x$ minimizes, and indeed maximizes, this expectation. As a result, we have to look at the situation in which the evidence imposes the constraint $Q(E) = 1-\varepsilon$ for $\varepsilon > 0$, and ask what happens as we let $\varepsilon$ approach 0. Then
$$\mathrm{Exp}_\mathfrak{L}((x, 1-\varepsilon-x, \varepsilon)|(p_1, p_2, p_3)) = -p_1\log x - p_2 \log (1-\varepsilon-x) - p_3 \log \varepsilon$$
Differentiating this with respect to $x$ gives
$$-\frac{p_1}{x} + \frac{p_2}{1-\varepsilon - x}$$
which equals 0 iff
$$x = (1-\varepsilon) \frac{p_1}{p_1 + p_2}$$
And this approaches Conditionalization as $\varepsilon$ approaches 0. So, in this sense, as Ben Levinstein pointed out, the local log inaccuracy measure gives Conditionalization, and indeed Jeffrey Conditionalization or Probability Kinematics as well (Levinstein 2012). So far, so good.
However, throughout this post, and in the two derivations above---the first concerning the Brier inaccuracy measure and the second concerning the local log inaccuracy measure---we assumed that all credence functions must be probability functions. That is, we assumed Probabilism, the other central tenet of Bayesianism alongside Conditionalization. Now, if we measure inaccuracy using the Brier measure, we can justify that, for then we have the accuracy dominance argument, which originated mathematically with Bruno de Finetti, and was given its accuracy-theoretic philosophical spin by Jim Joyce (de Finetti 1974, Joyce 1998). That is, if your prior or your posterior isn't a probability function, then there is an alternative that is and that is guaranteed to be more Brier-accurate. However, the local log inaccuracy measure doesn't furnish us with any such argument. One very easy way to see this is to note that the non-probabilistic credence function $(1, 1, \ldots, 1)$ over $\{w_1, \ldots, w_n\}$ dominates all other credence functions according to the local log measure. After all, $\mathfrak{L}((1, 1, \ldots, 1), w_i) = -\log 1 = 0$, for $i = 1, \ldots, n$, while $\mathfrak{L}(P, w_i) > 0$ for any $P$ with $p_i < 1$ for some $i = 1, \ldots, n$.
Another related issue is that the scoring rule $\mathfrak{l}$ that generates $\mathfrak{L}$ is not strictly proper. A scoring rule $\mathfrak{s}$ is said to be strictly proper if every credence expects itself to be the best. That is, for any $0 \leq p \leq 1$, $p\mathfrak{s}_1(x) + (1-p) \mathfrak{s}_0(x)$ is minimized, as a function of $x$, at $x = p$. But $-p\log x + (1-p)0 = -p\log x$ is always minimized, as a function of $x$, at $x = 1$, where $-p\log x = 0$. Similarly, an inaccuracy measure $\mathfrak{I}$ is strictly proper if, for any probabilistic credence function $P$, $\mathrm{Exp}_\mathfrak{I}(Q | P) = \sum^n_{i=1} p_i \mathfrak{I}(Q, w_i)$ is minimized, as a function of $Q$ at $Q = P$. Now, in this sense, $\mathfrak{L}$ is not strictly proper, since $\mathrm{Exp}_\mathfrak{L}(Q | P) = \sum^n_{i=1} p_i \mathfrak{L}(Q, w_i)$ is minimized, as function of $Q$ at $Q = (1, 1, \ldots, 1)$, as noted above. Nonetheless, if we restrict our attention to probabilistic $Q$, $\mathrm{Exp}_\mathfrak{L}(Q | P) = \sum^n_{i=1} p_i \mathfrak{L}(c, w_i)$ is minimized at $Q = P$. In sum: $\mathfrak{L}$ is only a reasonable inaccuracy measure to use if you already have an independent motivation for Probabilism. But accuracy-first epistemology does not have that luxury. One of central roles of an inaccuracy measure in that framework is to furnish an accuracy dominance argument for Probabilism.
So, we ask: is there a scoring rule $\mathfrak{s}$ and resulting inaccuracy measure $\mathfrak{I}$ such that:
- $\mathfrak{s}$ is a strictly proper scoring rule;
- $\mathfrak{I}$ is a strictly proper inaccuracy measure;
- $\mathfrak{I}$ furnishes an accuracy dominance argument for Probabilism;
- If $P(E) > 0$, then $\mathrm{Exp}_\mathfrak{I}(Q | P)$ is minimized, as a function of $Q$ among credence functions for which $Q(E) = 1$, at $Q(-) = P(-|E)$.
$$\mathfrak{l}^\star_0(x) = x\ \ \ \ \mathrm{and}\ \ \ \ \mathfrak{l}^\star_1(x) = -\log x + x-1$$
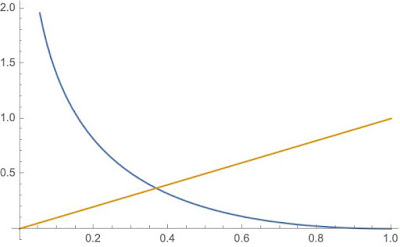 |
| The enhanced log score $\mathfrak{l}^\star$. $\mathfrak{s}_0$ in yellow; $\mathfrak{s}_1$ in blue. |
Before we state and prove the theorem, there are some features of this scoring rule and its resulting inaccuracy measure that are worth noting. Juergen Landes has identified this scoring rule for a different purpose (Proposition 9.1, Landes 2015).
Proposition 1 $\mathfrak{l}^\star$ is strictly proper.
Proof. Suppose $0 \leq p \leq 1$. Then
$$\frac{d}{dx} p\mathfrak{l}^\star_1(x) + (1-p)\mathfrak{l}^\star_0(x) = \frac{d}{dx} p[-\log x + x] + (1-p)x = -\frac{p}{x} + 1 = 0$$ iff $p = x$. $\Box$
Proposition 2 If $P$ is non-probabilistic, then $P^\star = \left (\frac{p_1}{\sum_k p_k}, \ldots, \frac{p_n}{\sum_k p_k} \right )$ accuracy dominates $P = (p_1, \ldots, p_n)$.
Proof. $$\mathfrak{L}^\star(P^\star, w_i) = -\log\left ( \frac{p_i}{\sum_k p_k} \right ) + 1 = -\log p_i + \log\sum_k p_k + 1$$ and $$\mathfrak{L}^\star(P, w_i) = -\log p_i + \sum_k p_k$$ But $\log x + 1 \leq x$, for all $x> 0$, with equality iff $x = 1$. So, if $P$ is non-probabilistic, then $\sum_k p_k \neq 1$ and $$\mathfrak{L}^\star(P^\star, w_i) < \mathfrak{L}^\star(P, w_i)$$ for $i = 1, \ldots, n$. $\Box$
Proposition 3 If $P$ is probabilistic, $\mathfrak{L}^\star(P, w_i) = 1 + \mathfrak{L}(P, w_i)$.
Proof.
\begin{eqnarray*}
\mathfrak{L}^\star(P, w_i) & = & p_1 + \ldots + p_{i-1} + (-\log p_i + p_i ) + p_{i+1} + \ldots + p_n \\
& = & -\log p_i + 1 \\
& = & 1 + \mathfrak{L}(P, w_i)
\end{eqnarray*}
$\Box$
Corollary 1 If $P$, $Q$ are probabilistic, then
$$\mathrm{Exp}_{\mathfrak{L}^\star}(Q | P) = 1 + \mathrm{Exp}_\mathfrak{L}(Q | P)$$
Proof. By Proposition 3. $\Box$
Corollary 2 Suppose $E_1, \ldots, E_m$ is a partition and $0 \leq q_1, \ldots, q_m \leq 1$ with $\sum^m_{i=1} q_i = 1$. Then, among $Q$ for which $Q(E_i) = q_i$ for $i = 1, \ldots, m$, $\mathrm{Exp}_{\mathfrak{L}^\star}(Q |P)$ is minimized at the Jeffrey Conditionalization posterior $Q(-) = \sum^k_{i=1} q_iP(-|E_i)$.
Proof. This follows from Corollary 1 and Theorem 5.1 from (Diaconis & Zabell 1982). $\Box$
Having seen $\mathfrak{l}^\star$ and $\mathfrak{L}^\star$ in action, let's see that they are unique in having this combination of features.
Theorem 1 Suppose $\mathfrak{s}$ is a strictly proper scoring rule and $\mathfrak{I}$ is the inaccuracy measure it generates. And suppose that, for any $\{w_1, \ldots, w_n\}$ and any $E \subseteq \{w_1, \ldots, w_n\}$, and any probabilistic credence function $P$, the probabilistic credence function $Q$ that minimizes the expected inaccuracy of $Q$ with respect to $P$ with the constraint $Q(E) = 1$, and when inaccuracy is measured by $\mathfrak{I}$, is $Q(-) = P(-|E)$. Then the scoring rule is
$$\mathfrak{s}_1(x) = -\log x +x\ \ \ \ \mbox{and}\ \ \ \ \mathfrak{s}_0(x) = x$$ or any affine transformation of this.
Proof. First, we appeal to the following lemma (Proposition 2, Predd, et al. 2009):
Lemma 1
(i) Suppose $\mathfrak{s}$ is a continuous strictly proper scoring rule. Then define$$\varphi_\mathfrak{s}(x) = -x\mathfrak{s}_1(x) - (1-x)\mathfrak{s}_0(x)$$Then $\varphi_\mathfrak{s}$ is differentiable on $(0, 1)$ and convex on $[0, 1]$ and $$\mathrm{Exp}_\mathfrak{I}(Q | P) - \mathrm{Exp}_\mathfrak{I}(P | P) = \sum^n_{i=1} \varphi_\mathfrak{s}(p_i) - \varphi_\mathfrak{s}(q_i) - \varphi_\mathfrak{s}^\prime (q_i)(p_i - q_i)$$ (ii) Suppose $\varphi$ is differentiable on $(0, 1)$ and convex on $[0, 1]$. Then let
- $\mathfrak{s}^\varphi_1(x) = - \varphi(x) - \varphi'(x)(1-x)$
- $\mathfrak{s}^\varphi_0(x) = - \varphi(x) - \varphi'(x)(0-x)$
Moreover, $\mathfrak{s}^{\varphi_\mathfrak{s}} = \mathfrak{s}$.
Now, let's focus on $\{w_1, w_2, w_3, w_4\}$ and let $E = \{w_1, w_2, w_3\}$. Let $p_1 = a$, $p_2 = b$, $p_3 = c$. Then we wish to minimize
$$\mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c))$$
Now, but Lemma 1,
\begin{eqnarray*}
&& \mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c)) \\
& = & \varphi(a) - \varphi(x) - \varphi'(x)(a-x)\\
& + & \varphi(b) - \varphi(y) - \varphi'(y)(b-y) \\
& + & \varphi(c) - \varphi(1-x-y) - \varphi'(1-x-y)(c - (1-x-y)) \\
& + & \mathrm{Exp}_\mathfrak{I}((a, b, c, 1-a-b-c) | (a, b, c, 1-a-b-c))
\end{eqnarray*}
Thus:
\begin{eqnarray*}
&& \frac{\partial}{\partial x} \mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c))\\
& = & \varphi''(x)(x-a) - ((1-x-y) - c) \varphi''(1-x-y)
\end{eqnarray*}
and
\begin{eqnarray*}
&& \frac{\partial}{\partial y} \mathrm{Exp}_\mathfrak{I}((x, y, 1-x-y, 0) | (a, b, c, 1-a-b-c))\\
& = & \varphi''(y)(y-b) - ((1-x-y) - c) \varphi''(1-x-y)
\end{eqnarray*}
which are both 0 iff$$\varphi''(x)(x-a) = \varphi''(y)(y-b) = ((1-x-y) - c) \varphi''(1-x-y)$$ Now, suppose this is true for $x = \frac{a}{a+b+c}$ and $y = \frac{b}{a + b+ c}$. Then, for all $0 \leq a, b, c \leq 1$ with $a + b + c \leq 1$, $$a\varphi'' \left ( \frac{a}{a+b+c} \right ) = b\varphi'' \left ( \frac{b}{a+b+c} \right ) $$
We now wish to show that $\varphi''(x) = \frac{k}{x}$ for all $0 \leq x \leq 1$. If we manage that, then it follows that $\varphi'(x) = k\log x + m$ and $\varphi(x) = kx\log x + (m-k)x$. And we know from Lemma 1:
\begin{eqnarray*}
& & \mathfrak{s}_0(x) \\
& = & - \varphi(x) - \varphi'(x)(0-x) \\
& = & - [kx\log x + (m-k)x] - [k\log x + m](0-x) \\
& = & kx
\end{eqnarray*}
and
\begin{eqnarray*}
&& \mathfrak{s}_1(x) \\
& = & - \varphi(x) - \varphi'(x)(1-x) \\
& = & - [kx\log x + (m-k)x] - [k\log x + m](1-x) \\
& = & -k\log x + kx - m
\end{eqnarray*}
Now, first, let $f(x) = \varphi''\left (\frac{1}{x} \right )$. Thus, it will suffice to prove that $f(x) = x$. For then $\varphi''(x) = \varphi''\left (\frac{1}{\frac{1}{x}} \right ) = f \left ( \frac{1}{x} \right ) = \frac{1}{x}$, as required. And to prove $f(x) = x$, we need only show that $f'(x)$ is a constant function. We know that, for all $0 \leq a, b, c \leq 1$ with $a + b + c \leq 1$, we have
$$a f \left ( \frac{a + b + c}{a} \right ) = bf \left ( \frac{a + b + c}{b} \right )$$
So$$
\frac{d}{dx} a f \left ( \frac{a + b + x}{a} \right ) = \frac{d}{dx} bf \left ( \frac{a + b + x}{b} \right )
$$So, for all $0 \leq a, b, c \leq 1$ with $a + b + c \leq 1$
$$
f'\left (\frac{a+b+c}{a} \right ) = f'\left (\frac{a + b + c}{b} \right )
$$We now show that, for all $x \geq 1$, $f'(x) = f'(2)$, which will suffice to show that it is constant. First, we consider $2 \leq x$. Then let
$$a = \frac{1}{x}\ \ \ \ \ b = \frac{1}{2}\ \ \ \ \ c = \frac{1}{2}-\frac{1}{x}$$
Then
$$f'(x) = f'\left (\frac{a + b + c}{a} \right ) = f'\left (\frac{a + b + c}{b} \right ) = f'(2)$$
Second, consider $1 \leq x \leq 2$. Then pick $2 \leq y$ such that $\frac{1}{x} + \frac{1}{y} \leq 1$. Then let
$$a = \frac{1}{x}\ \ \ \ \ b = \frac{1}{y}\ \ \ \ \ c = 1 - \frac{1}{x} - \frac{1}{y}$$
Then
$$f'(x) = f'\left (\frac{a + b + c}{a} \right ) = f'\left (\frac{a + b + c}{b} \right ) = f'(y) = f'(2)$$
as required. $\Box$

Comments
Post a Comment